C#和.Net框架

线性结构查找

• 顺序查找
• 折半查找
• 分块查找

B树

动机

• 多级存储系统中使用B-树,可针对外部查找，大大减少I/O次数
  • 对于普通的AVL树来说，在1G个记录中进行查找,平均需要30次I/O操作,并且每次只能读取一个关键码
  • 对于b树来说，充分利用外存对批量访问的高效支持，将此特点转换为有点
    • 每下降一层，都以超级节点为单位，读入一组关键码

超级结点

• B树的超级结点等价于二叉搜索树中经过适当合并得到的结点

定义

• 所谓m阶b树,即m路平衡搜索树(m >=2)
• 外部节点的深度统一相等,所有叶结点的深度统一相等
  • 外部节点用于沟通不同级别的存储介质
• 树高h = 外部节点的深度
• 对于内部节点的最大值
  • 不超过m-1个关键码
  • 不超过m个分支
• 对于内部节点的最小值
  • 树根m >= 2
  • 其余m >= ceil(m/2)

---

• 也可以称m阶b树为(ceil(m/2),m)-树

b树的高度

• b树的高度对应磁盘的存取次数,对于包含n个关键码、高度为h、阶数为m的b树 $$h_{max} >= log_{m}{(n+1)}$$ $$h_{max} <= log_{ceil(m/2)}{((n+1)/2)}+1$$

b树的插入

定位

• 通过查找算法,找到失败位置,这个失败位置就是插入位置

  插入(2种情况)

  普通插入

• 插入后关键码的个数 < m 则直接插入

  分裂

• 插入后关键码的个数 = m 则需要进行分裂.
• 进行分裂时,取中间的结点插入到父节点,然后产生两个新的超级结点
• 然后一次检查父节点,如果分裂超过传到到树根，则b树高度增加1

删除（3种情况）

普通删除

• 如果删除相应关键字后，超级结点的关键码个数>= ceil(m/2) - 1,则直接删除该关键字

  兄弟够借（旋转）

• 如果删除相应关键字后，超级结点的关键码个数< ceil(m/2) - 1,且此时他的左右兄弟结点中的关键码个数>= ceil(m/2).
• 此时采用旋转，父节点向下溢结点借出结点,父节点向下溢的兄弟结点要一个结点,注意要保证中序遍历的顺序性

兄弟不够借（合并）

• 如果删除相应关键字后，超级结点的关键码个数< ceil(m/2) - 1,且此时他的左右兄弟结点中的关键码个数= ceil(m/2)-1.
• 此时采用合并操作,对于合并操作父节点会减少一个关键码，因此需要依次检查相应结点,如果传导到树根则b树高度减1

B+树

B+树需要满足的条件

• 每个分支最多m根子树(孩子结点)
• 根结点最少2根子树,分支结点至少ceil(m/2)根子树
• 结点的子树个数与关键字个数相等
• 所有叶结点包含所有关键字及对应记录的指针,按大小排序且相互链接起来
• 分支结点仅保存子节点中关键字的最大值及指向子节点的指针

m阶b树和b+树的区别

• 关键码和子树的关系
  • B+:n个关键码对应n根子树
  • B-:n个关键码对应n+1根子树
• 关键字范围
  • B+: ceil(m/2) <= n <= m ( 根 : 1 <= n <= m)
  • B-: ceil(m/2)- <= n <= m-1 ( 根 : 1 <= n <= m-1)
• 结点存储信息
  • B+ : 叶结点包含所有信息,分支结点仅起索引作用
  • B- : 每个结点都保存信息
• 叶结点关键字
  • B+ : 叶结点包含所有关键字
  • B- : 结点关键字不重复

红黑树

参考:学堂在线,邓俊辉,数据结构

动机

• 持久性(一致性)结构：支持对历史版本的访问
  T.serach(ver(版本号),key)

• 蛮力实现:每个版本独立保存,各版本入口自成一个搜索结构.

单次操作o(logh + logn),累计o(hn)时间和空间,累计空间复杂度是o(hn)是因为每次都要保存前一个版本的结点 // h = |history|

• O(1)重构:对树形结构的拓扑而言,相邻版本之间的差异不能超过O(1)
  • 任何一次动态操作引发的结构变化量不超过O(1)

    红黑树概念

• 红黑树是由红、黑两类结点组成的BST(统一增设外部结点NULL,使之成为真二叉树)

  真二叉树:所有节点的度都要么为0，要么为2。

  • 1.树根:必为黑色
  • 2.外部结点:均为黑色
  • 3.其余结点:若为红、则只能有黑孩子(当前结点为红,其父亲结点和孩子结点都为黑)
  • 4.外部结点到根:途中黑结点数据相等(黑深度)

---

• 性质3.作用:红色结点经过提升变换后(将黑色结点提高到与黑父亲同一高度的位置,类似b树)之后,所有叶子结点都在同一层.
  • 提升后的红黑树就是4阶b树(2,4-树)

红黑树操作接口

template <typename T> calss RedBlack : public BST<T>{
public:
    //BST::Serach()的其余接口都可直接沿用
    BinNodePosi(T) insert(const T& e);//插入
    bool remove(const T& e );//删除
protected:
    void solveDoubleRed(BiNodePosi(T) x);//双红修正
    void solveDoubleBlack(BiNodePosi(T) x);//双黑修正
    int updateHeight(BinNOdePosi(T) x);//更新结点x的高度(黑高度)
};

红黑树插入

* 现拟插入关键码e //T中不含e
* 按照BST的常规算法,插入之 // x = insert(e)必为末端结点
    * 不妨设x的父亲p = x->parent存在 //否则,即平凡的首次插入
* 将x染红(除非它是根)
    * 此时条件1,2,4必然满足

情况1:插入结点为根结点

• 此时染为黑色

情况2:插入结点不为根结点

情况2.1:插入结点的父亲结点p为黑色.

• 此时满足条件3,保持为红色

  情况2.2:插入结点的父亲结点p为红色.

• 此时不满足条件3:产生双红缺陷
  • 此时需要考虑该节点的叔叔结点(祖先结点的另一个孩子)

情况2.2.1:叔叔结点为黑色(包括叔叔结点为外部（也是黑色）结点)

情况2.2.1.1:插入结点为父亲结点的左孩子,并且父亲结点是爷爷结点的左孩子(LL) || 插入结点为父亲结点的右孩子,并且父亲结点是爷爷结点的右孩子(RR)

• 以LL为例,将红色结点都向上提升,形成(a’)的4阶b树,可以看到.按照规则,含有3个关键字的四阶b树,其关键字如果含有2个红色结点,必然为RBR结构.
• 所以只需要按照图中结构,让p变为黑,g变为红即可.

情况2.2.1.2:插入结点为父亲结点的左孩子,并且父亲结点是爷爷结点的右孩子(LR) || 插入结点为父亲结点的右孩子,并且父亲结点是爷爷结点的左孩子(RL)

• 以RL为例,将红色结点都向上提升,形成(B’)的4阶b树按照规则,含有3个关键字的四阶b树,其关键字如果含有2个红色结点,必然为RBR结构.
  
• 并且要求该子结构为如图c和c’的类型.

• 一次需要先对x结点做左旋操作,然后再按照(a’)方式进行染色.（即x为黑,g为红）

---

• 通过b树来理解双红缺陷(黑叔叔)
  • 在某个三叉结点中插入红关键码,使得原黑关键字不再居中.
    • RRB or BRR,出现相邻的红关键码

情况2.2.2:叔叔结点为红色

情况2.2.2.1:插入结点为父亲结点的左孩子,并且父亲结点是爷爷结点的左孩子(LL) || 插入结点为父亲结点的右孩子,并且父亲结点是爷爷结点的右孩子(RR)

• 以LL为例,将红色结点向上提升,形成(a’)的b书,可以看到该4阶b树发生了上溢,需要按照b树的规则对其进行分裂.所以将红黑树中的双红缺陷转换为了b树中的上溢缺陷.

• 对a对应的b树做分裂操作,如图(c’),将中间结点(即染为红色)提升,剩下的左右子孩子,将中间关键字染为红色,周围关键字染为黑色.

• 同样,将g结点提升之后需要考虑g的父亲结点是否会产生双红缺陷.重复考虑类似的插入操作.

情况2.2.2.2:插入结点为父亲结点的左孩子,并且父亲结点是爷爷结点的右孩子(LR) || 插入结点为父亲结点的右孩子,并且父亲结点是爷爷结点的左孩子(RL)

• 以RL为例,类似于情况2.2.2.1.

---

• 总结
  • 重构,染色操作均属于常熟时间的局部操作,股只需统计总次数.
  • 红黑树的每一次插入操作都可在o(logn)时间内完成
  • 其中至多做: o(logn)次结点染色,一次旋转操作.

情况	旋转次数	染色次数	此后
uncle为黑	1	2	调整随机完成
uncle为红	0	3	可能再次双红,但必上升两层.

• 流程图

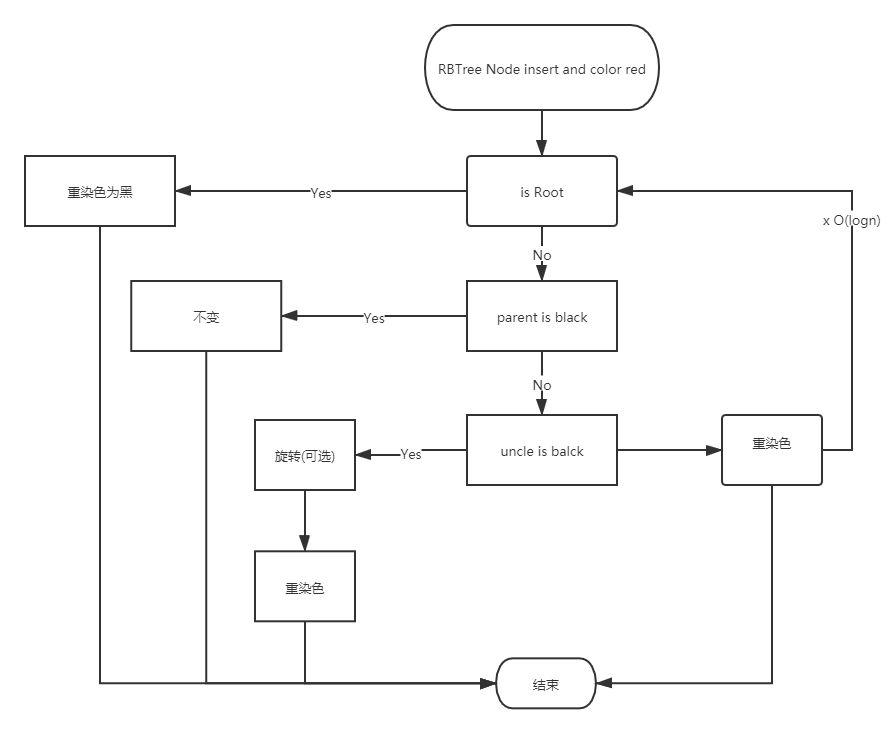
红黑树删除

* 首先按照BST常规算法,执行:
    r = removeAt(x,_hot)
* x由孩子r接替
    // 另一个孩子记为w(即黑的NULL)
* 此时条件1,2,依然满足,不3,4不一定满足
    * 若x和r之一是红的,那3,4不难解决

情况1: 删除结点x和孩子r,两者之一为红色

• 这是只要将接替的r结点染为黑色即可.
  

情况2:删除结点x和孩子r均为黑色

• 此时会发生双黑缺陷,摘除x并代之以r后,全树黑深度不再统一,对应b树中x所属结点产生下溢.
• 此时需要在新树中中考察x的父亲结点p,以及r的兄弟结点s.总共考虑4中情况

情况2.1:s为黑,且至少有一个红孩子t

• 变换方法:
  • 将p结点由旋转
  • 此为,保持r为黑色,t和p染为黑色,s继承原来p的颜色.
• 底层原理:
  • 将图(a)进行向上提升后,可以看出删除x结点后发生了下溢.
  • 通过关键码的旋转,可以消除结点的下溢.

情况2.2:s为黑,且两个孩子均为黑;p为红.

• 变换方法:
  • r保持黑;s转红;p转黑
• 底层原理:
  • 将(a)提升后,如图(a’)发生下溢,但是无法向相邻的结点借关键码,所以采用合并操作.
  • 对于取出的关键码p因为不在会被向上提升所以为黑色,结点中的关键码只存在RBR,RB,BR三种情况,所以s为红色.
  • 红黑树的性质因此在全局得以恢复
  • 失去关键码p后,上层结点不会继续下溢.
    • 因为合并之前,在p之左或右侧还应有(问号)关键码,必维黑色.有且仅有一个.

情况2.3:s为黑,且两个孩子均为黑;p为黑.

• 变换方法:
  • s转红,r和p保持黑
  • 依次处理上层结点的下溢.

• 底层原理:
  • 将(a)提升后,如图(a’)发生下溢,但是无法向相邻的结点借关键码，而此时上层结点只有一个关键码,在借出关键码之后,上层结点会再次导致下溢,需要重复操作.

情况2.4:s为红(其两个孩子必为黑)

• 变换方法:
  • 将p点向右旋转,s边黑,p变红
  • 转换为2.1,2.2的情况
• 底层原理:
  • 将(a)提升后,如图(a’)会发生下溢,且s’结点为黑,所以只能合并,需要向上层借一个关键码,则需要对上层结点重新染色.s为黑,p为红.
  • 此时r有了一个新的黑兄弟s’,且p为红,所以此时就会转换到2.1和2.2的情况.

---

• 总结:
  • 红黑树的每一次操作的时间为O(log(n))

情况	旋转次数	染色次数	此后
(1)兄弟为黑,有红孩子t	1	3	调整随即完成
(2)兄弟为黑,无红黑子,父亲结点为红	0	2	调整随即完成
(3)兄弟为黑,无红黑子,父亲结点为黑	0	1	必然再次双黑,但将上升一层.
(4)兄弟为红	1	2	转换为(1)或2(R)

散列表(哈希表)

• 散列函数:一个把查找表中的关键字映射成该关键字对应的地址的函数,记为
  • Hash(key) = Addr
• 冲突:散列函数可能会把两个或两个以上的不同关键字映射到同一地址
  • 原因：散列值是非负整数，总量是有限的，但是现实世界中要处理的键值是无限的，将无限的数据映射到有限的集合，肯定避免不了冲突。
• 同义词:发生碰撞的不同关键字
• 散列表:根据关键字而直接进行访问的数据结构散列表建立了关键字和存储地址之间的一种直接映射关系.

散列函数的构造方法

• 散列函数的特点
  • 定义域包括全部需要存储的关键字,值域取决于散列表的大小或地址范围
  • 散列函数计算出来的地址应该等概率、均匀地分布在整个地址空间内,减少冲突的发生.
  • 散列函数应该尽量简答,能够在短时间内计算出任意关键字的散列地址.

---

• 直接定址法 : H(key) = key or H(key) = a * key + b

  • 取关键字的某个线性函数值作为散列地址
  • 均匀也不会产生冲突
  • 适合查找表较小且连续的情况,不连续会造成空间浪费

• 除留余数法: H(key) = key % p

  • p为不大于散列表长m但最接近或等于m的质数
  • p决定了造成冲突的可能性

• 数字分析法:

  • 如果关键字是位数较多的数字，且这些数字部分存在相同规律则可以采用抽取剩余不同规律部分作为散列地址
  • 例如手机:前3位接入号,中间4位HLR识别号,后4位用户号,选择后四位作为散列地址就是不错的选择
  • 可以对这些抽出来的数字进行反转,左移,右移等操作
    • 目的：尽量合理地将关键字分配到散列表的各个位置
  • 适合处理关键字位数比较大的情况,事先知道关键字的分布且关键字的若干位分布较均匀.

• 平方取中法:

  • 即取关键字平方的中间位数作为散列地址
  • 例如:比如假设关键字是 4321，那么它的平方就是 18671041，抽取中间的 3 位就可以是 671，也可以是 710，用做散列地址
  • 适合于不知道关键字的分布，而位数又不是很大的情况

• 折叠法:

  • 折将关键字从左到右分割成位数相等的几部分（注意最后一部分位数不够时可以短些,然后将这几部分叠加求和,并按散列表表长，取后几位作为散列地址
  • 例如:比如假设关键字是 9876543210，散列表表长为三位,则我们可以将它分为四组 987|654|321|0,然后将它们叠加求和 987+654+321+0=1962,再取后 3 位得到散列地址即为 962
  • 折叠法事先不需要知道关键字的分布，适合关键字位数较多的情况

• 随机数法: H(key) = random(key)

  • 取关键字的随机函数值为它的散列地址
  • 当关键字的长度不等时采用这个方法构造散列函数是比较合适的

处理冲突的方法

• 任何散列函数都不能绝对地避免冲突.需要为发生冲突的关键字寻找下一个Hash地址.
• Hi表示处理冲突中第i次探测得到的散列地址.

开放定址法

• 开放定址法:可存放新关键字的空间地址既向它的同义词表项开放,又向她的非同义词表项开放.
  • $H_{i} = (H(key) + d_{i})$ % m
    • m为散列表长
    • $d_{i}$为增量序列

---

• 线性探测法

  • $d_{i}$ = 0,1,2,…,m-1
  • 冲突发生时,顺序查看表中下一个单元(循环探测),直到找到一个空闲单元或查遍全表
  • 问题:容易造成大量元素在相邻的散列地址上聚集起来,大大降低了查找效率
    • 使得第i个散列地址的同义词存入i+1个散列地址,本应存入第i+1个散列地址的元素只能存入第i+2个散列地址.

• 平方(二次)探测法

  • $d_{i} = 0^{2},1^{2},-1^{2},2^{2},-2^{2},…,k^{2},-k^{2}$
    • k <= m/2
    • m 必须是一个可以表示成4k+3的素数
  • 避免堆积问题,但不能探测散列表上的所有元素,但至少能探测到一半单元

• 再散列法

  • $d_{i} = Hash_{2}(key)$
  • $H_{i} = (H(key)+i*Hash_{2}(key))%m
  • 第一个散列函数用于得到地址,当发生冲突时使用第二个散列函数

• 伪随机序列法

  • $d_{i} = 伪随机序列$

---

• 在开放定址法中,不能物理删除已有元素,会阶段其他具有相同散列地址的元素.
• 只能利用删除标记做逻辑删除
• 需要定期维护散列表

拉链法

• 把同义词存储在一个线性链表中,这个线性链表由其散列地址唯一识别.
• 拉链法适用于经常进行插入和删除的情况.